Test sobre resolución de problemas (hacedlo y me contáis)

Es que los experimentos se hacen teniendo eso en mente.

Uno no monta un experimento para falsar la teoría de la relatividad utilizando velocidades en las que la teoría gravitacional de Newton se cumple, te vas a velocidades cercanas a la luz. Cuanto más puñetero seas contra tu teoría más reforzada sale si lo supera.

Esta claro que probar es lo mejor para acertar, pero yo pensaba que era como un examen, es decir, un test donde dar la respuesta y no probar

Si pensabas que era un examen entonces no leíste la pregunta

Pues mi primera prueba ha sido 1 - 3 - 5. Bien, pues he probado 8 - 10 - 12 y ahí ya he dicho, pues sumar dos al de antes

Curioso, sí. Espero recordar la lección para el futuro

Y yo que me pensaba que solo había un intento, la he cagado pero bien...

Me consuela pensar que no he tenido reparos en poner secuencias con la pretensión de que fallaran para descartar posibles reglas. Como siete "Noes" he obtenido para ir eliminando hipótesis :) Pero soy un zote, no he llegado a resolverlo más allá de suponer que el 2º tenía que ser mayor que el 1º y dar por hecho que el tercer número era el resultado de alguna operación con los dos anteriores. Me he quedado a las puertas XD

Deschamps escribió:Me consuela pensar que no he tenido reparos en poner secuencias con la pretensión de que fallaran para descartar posibles reglas. Como siete "Noes" he obtenido para ir eliminando hipótesis Pero soy un zote, no he llegado a resolverlo más allá de suponer que el 2º tenía que ser mayor que el 1º y dar por hecho que el tercer número era el resultado de alguna operación con los dos anteriores. Me he quedado a las puertas

Has superado el test con honores, tío. El objetivo no era acertar la regla, era dar secuencias buscando un no.

Bou escribió:Has superado el test con honores, tío. El objetivo no era acertar la regla, era dar secuencias buscando un no.

Que va. Posiblemente se deba a las metodologías a las que estoy acostumbrado, donde explorar resultados negativos es tan necesario como con los positivos. Como siempre se explica en análisis, para descartar una suposición es suficiente encontrar un contraejemplo, y en esas estuve.

Pero reconozco que también de forma irracional asumí como válidas muchas condiciones (que debían ser números naturales, que el tercero se obtenía manipulando los dos anteriores de algún modo, ...).

Muy interesante el experimento XD

Bou escribió:
Me encanta la forma tan sencilla en que expone por qué hay que evitar el sesgo de confirmación:

En el viejo mundo tenían la teoría de que los cisnes eran siempre blancos, y con cada cisne blanco que veían se convencían más. No salieron de su error hasta llegar a Australia y encontrar cisnes negros allí. No se puede demostrar que una teoría es cierta, solo que no lo es.

Eso es lo importante del método científico: intentamos desmentir nuestras teorías, y si no lo logramos es cuando podemos empezar a decir que deben de tener algo de verdad.

Hagamos lo mismo en el día a día: si estás convencido de que algo es verdad, haz lo que puedas por desmentirlo. Solo así podrás acercarte a la verdad sin engañarte a ti mismo.

Lo de los cisnes negros es la explicacion que dio Popper para el Falsacionismo, que luego fue continuada por Lakatos (entre otros)

https://es.wikipedia.org/wiki/Falsacionismo

http://recuerdosdepandora.com/reflexion ... dociencia/

https://aquileana.wordpress.com/2008/04 ... es-negros/

Creo que soy raro...
Yo necesitaba los no's para confirmar que mi idea era correcta. Primero he probado números primos impares, luego seguidos, luego mayores que cien, luego invertidos (2 veces), luego mucho más grandes, luego incrementados pero negativos, luego al a inversa, luego iguales, y luego otra vez incrementados enormes.... de ahí he deducido la norma... Y realmente lo que buscaba eran la respuesta negativa sabiendo que se alejaba de mi teoria.

A mi no me ha sorprendido, pero también es cierto que estoy muy acostumbrado a este tipo de problemas.

Yo soy programador, y si tengo que programar algo así, tengo que hacer pruebas unitarias (donde pruebo el funcionamiento). Así que tendría que probar combinaciones buenas, y también combinaciones incorrectas para demostrar que mi código es correcto.

Esto es lo mismo, solo que el "código" es una idea en mi cabeza.

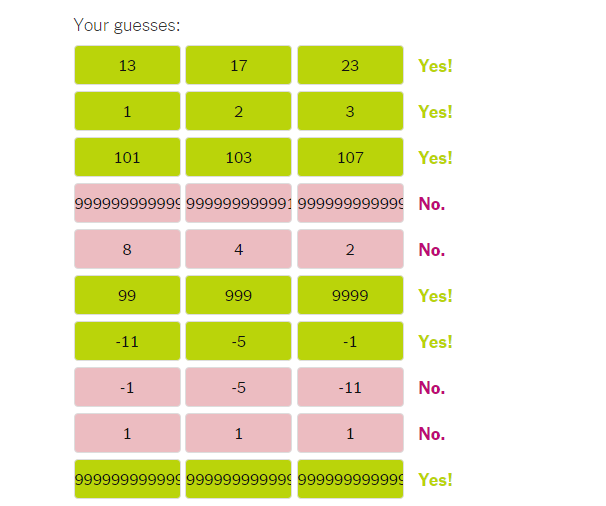
Yo personalmente no me fijé en que eran dobles (estaría dormido). Primero pensé que eran pares, así que probé más pares, funciona. Probé impares, funciona, probé un 0 y no funcionaba. ¿Enteros positivos? Probé -1 y funcionó. ¿Todo menos 0? Probé números primos y falló. Luego probé otros primos pero en orden y funcionó. Ya me di cuenta del problema.

Es cierto lo que cuenta el texto que no nos gusta el no, pero precisamente a los programadores si nos gusta, ya que necesitamos ese "no" para saber que estamos haciendo las cosas bien.